Inequalities and Absolute Value

Section 3 Inequalities and Absolute Value

Subsection 3.1 Inequalities

Inequalities are a crucial tool for studying the real numbers. And even for constructing them in the first place! For example, even if we do not yet know that there is a real number called “square-root-of-two”, we do know that we can define a subset of rational numbers consisting of all those whose square is less than two:

$\begin{equation*} A = \bigl\{ x\in \mathbb{Q} \colon x^2 \lt 2 \bigr\}. \end{equation*}$

🔗

While this set doesn't have a maximum (greatest element), we get the sense that if it did, that greatest element would be the number we should call

$\sqrt{2}\text{.}$

🔗

Sets like the one above can be used to construct the real numbers. Then, once we've done so, we see they are part of the important class of subsets of the real numbers called intervals.

🔗

Definition 3.1. Interval.

A subset $I\subseteq\mathbb{R}$ is called an interval if, for all $x,y,z\in\mathbb{R}$ with $x \leq y \leq z\text{,}$ we have

$\begin{equation*} \text{If }x,z\in I \text{ then }y\in I. \end{equation*}$

If an interval has finite upper and lower bounds $a,b\in\mathbb{R}$ respectively, we use one of the following notations for it:

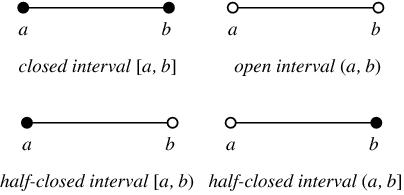
Figure Notations for intervals with endpoints $a,b\text{.}$ Source: MathWorld

🔗

Intuitively, an interval is a subset of the real numbers that has “no gaps” in it. Often, we define functions on domains made of unions of intervals, on each of which the function's definition may be different. These are called piecewise functions.

🔗

Remark 3.3.

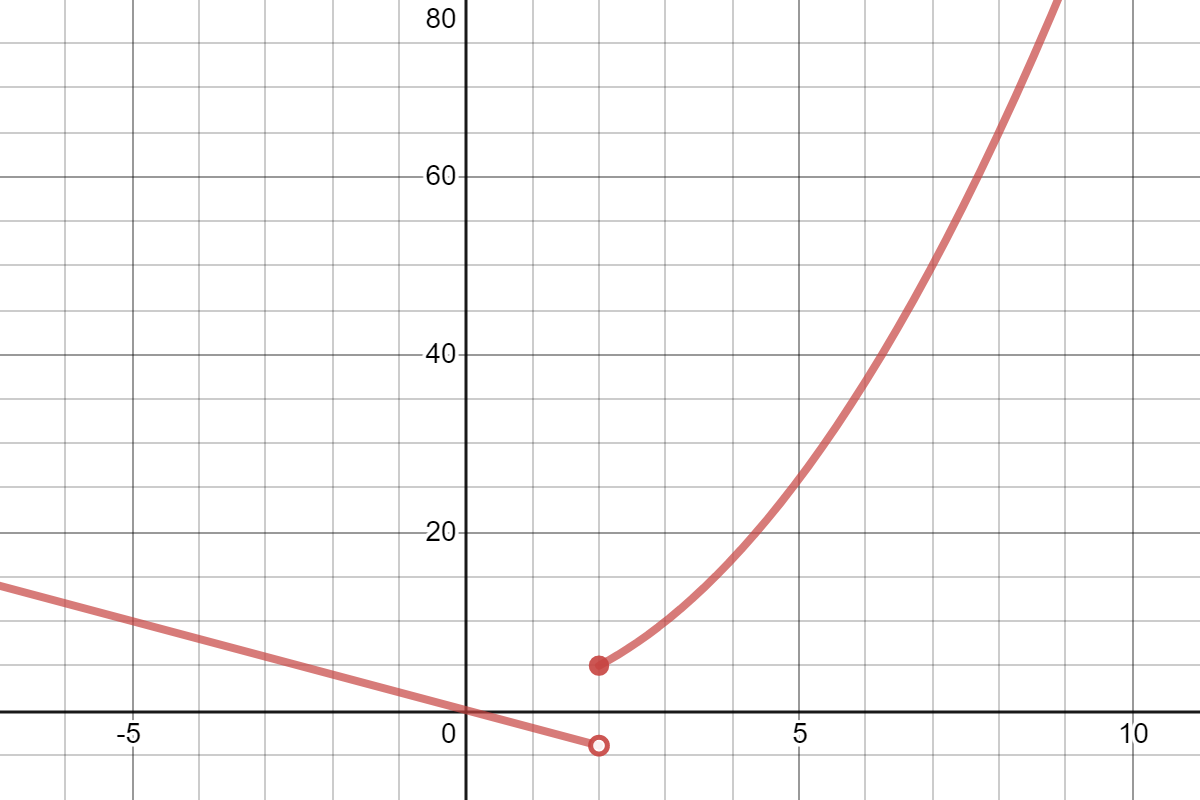
Graph the piecewise function $f(x) = \begin{cases}-2x &,\text{ when } x\lt 2\\ x^2+1 &,\text{ when }x\geq 2\end{cases}\text{.}$

On the interval $I_1 = (-\infty,2)\text{,}$ the function has definition $f(x)=-2x\text{:}$

Figure 3.4. A graph of

$f(x)$ restricted to

$I_1=(-\infty,2)$

On the interval $I_2 = [2,\infty)\text{,}$ the function has definition $f(x)=x^2+1\text{:}$

Figure 3.5. A graph of

$f(x)$ restricted to

$I_2=[2,\infty)$

Putting both pieces on the same graph, and using carefully an open circle to depict a point where this graph is not, we get the completed graph of $f\text{:}$

Figure A graph of the piecewise function $f(x)\text{.}$

🔗

Subsection 3.2 Absolute Value

🔗

Whenever we have an “origin” in mathematics, it's often helpful to be able to measure our distance to that origin. In vector spaces like

$\mathbb{R}^3\text{,}$ we can measure the distance to the origin

$(0,0,0)$ using a norm function such as the one that measures straight-line (Euclidean) distance:

$\begin{gather} \bigl\| (x,y,z) \bigr\| = \sqrt{ x^2+y^2+z^2 }.\label{eq_threenorm}\tag{3.1} \end{gather}$

🔗

We won't need so many dimensions to study real analysis (at least, not in the first semester). We only need one: a single real number

$x\in \mathbb{R}^1\text{,}$ and a norm which we denote with the single bar

$|x|\text{.}$ Equation (3.1) simplifies into a definition that we call the absolute value of

$x\text{,}$ as follows.

🔗

Definition 3.7. Absolute Value.

Let $x\in \mathbb{R}$ be a real number. The absolute value of $x$ is denoted by $|x|\text{,}$ and is defined by

$\begin{align} |x| = \sqrt{\, x^2\, } = \begin{cases} -x&\text{ when }x\lt 0\\ x&\text{ when }x \geq 0\end{cases}\label{eq_absolutevalue}\tag{3.2} \end{align}$

🔗

Intuitively, we may think of

$|x|$ as “the nonnegative version of

$x$ ”. It may help in Equation (3.2) to read

$-x$ as “the opposite of

$x$ ” to remind yourself why this is.

🔗

The following properties apply to absolute values of real numbers. (In fact, all but (3.6) are properties of “norm functions” in general, wherever they are defined.)

🔗

Theorem 3.8. Properties of Absolute Value.

Let $a,b\in\mathbb{R}$ be real numbers, and let $c\geq 0\text{.}$ Then

$\begin{align} |a| &\geq 0 && \textsf{(Positivity)}\tag{3.3}\\ |a| &= 0 \text{ if and only if }a=0 && \textsf{(Nondegeneracy)}\tag{3.4}\\ |ab| &= |a|\cdot |b| && \textsf{(Homogeneity)}\label{eq_homogeneity}\tag{3.5}\\ |a| &\leq c \text{ if and only if }-c \leq a \leq c \label{eq_abseq}\tag{3.6}\\ |a+b| &\leq |a| + |b| && \textsf{(Triangle inequality)}\label{eq_triangle}\tag{3.7} \end{align}$

🔗

A special case of Equation (3.5) is that

$|-a| = |a|\text{,}$ just by taking

$b=-1\text{.}$

🔗

The triangle inequality, Equation (3.7), is one of the most valuable tools (without exaggeration -- you will use it all the time) in real analysis. It has several corollaries and alternative forms that can be used as well.

🔗

Corollary 3.9. Triangle Inequalities.

Let $a,b\in\mathbb{R}$ be real numbers. Then

$\begin{align} |a+b| &\leq |a|+|b| && \textsf{(Triangle inequality)}\tag{3.8}\\ |a-b| &\geq \biggl| \,|a| - |b|\, \biggr| && \textsf{(Reverse triangle inequality)}\tag{3.9}\\ |a|-|b| \leq |a+b| &\leq |a|+|b|\tag{3.10} \end{align}$

Furthermore, for any natural number $n\geq 2$ and real numbers $a_1,a_2,a_3,\ldots,a_n\in\mathbb{R}\text{,}$ we have

$\begin{equation*} \bigl|a_1+a_2+a_3+\cdots+a_n\bigr| \leq |a_1|+|a_2|+|a_3|+\cdots+|a_n|. \end{equation*}$

🔗

Subsection 3.3 Solving Inequalities

🔗

Many real analysis students find that solving an inequality, as opposed to solving an equation, is an essential skill that they haven't had enough practice doing. There are several different approaches to solving inequalities, especially when they involve absolute values as they will in our course; another approach might be to solve them graphically.

🔗

We'll focus on how to solve inequalities by applying at each step a (one-to-one) function to each side. For example, we want to think of the step

$\begin{align*} 19x-12 &\lt 45\\ \color{cyan}{+12}& \;\; \color{cyan}{+12} && \text{"add 12 to both sides"}\\ 19x &\lt 57 \end{align*}$

🔗

as, instead, the application of the function

$f(x)=x+12$ to both sides:

$\begin{align*} 19x-12 &\lt 45\\ \color{cyan}{f({}}19x-12\color{cyan}{{})} & \;\; \color{cyan}{f({}} 45 \color{cyan}{{})} && \text{"Apply }f(x)=x+12\text{ to both sides"}\\ 19x &\lt 57. \end{align*}$

🔗

This is useful because it reminds us which steps reverse the inequality sign, as follows.

🔗

Definition 3.10. Increasing and Decreasing Functions.

Let $f\colon \mathbb{R}\to\mathbb{R}$ be a function.

We call $f$ an increasing function if it preserves the sense of inequalities. That is,

$\begin{gather} \text{For all }x,y\in\mathbb{R}\text{, if } x \leq y \text{ then } f(x) \leq f(y).\label{eq_inc}\tag{3.11} \end{gather}$

We call $f$ a decreasing function if it reverses the sense of inequalities. That is,

$\begin{gather} \text{For all }x,y\in\mathbb{R}\text{, if } x \leq y \text{ then } f(x) \geq f(y).\label{eq_dec}\tag{3.12} \end{gather}$

🔗

When we solve an inequality, at each step we're applying a (one-to-one) function to both sides. So, Definition 3.10 is critical to remember since it tells us whether we need to keep the inequality sign as it is (if the function we applied is increasing), or flip the inequality sign (if the function we applied is decreasing). The following two examples show how we can keep track.

🔗

Remark 3.11.

Solve the inequality $\bigl|2x+4\bigr| \lt 3\text{.}$

Step by step, here is a solution method:

$\begin{align*} &|2x+4| \lt 3 && \\ -3\lt{} & 2x+4 \lt 3 && \knowl{./knowl/eq_abseq.html}{\text{(3.6)}}\\ -7 \lt{} & 2x \lt -1 && \text{Via }f(x)=x-4\text{, increasing }\knowl{./knowl/eq_inc.html}{\text{(3.11)}}\\ -\frac72 \lt{} & x \lt -\frac12 && \text{Via }f(x)=x/2\text{, increasing }\knowl{./knowl/eq_inc.html}{\text{(3.11)}} \end{align*}$

According to Definition 3.1 we can express our answer as the open interval $\left(-\frac72,-\frac12\right)\text{.}$

🔗

Remark 3.12.

Solve the inequality $\displaystyle\frac{1}{6x-2x^2} \leq \displaystyle-\frac{1}{20}\text{.}$

Step by step, here is a solution method. Pay careful attention to when and why the inequality sign switches!

$\begin{align*} \displaystyle\frac{1}{6x-2x^2} &\leq \displaystyle-\frac{1}{20} && \\ 6x-2x^2 &\geq -20 && \text{Via }f(x)=1/x\text{, decreasing }\knowl{./knowl/eq_dec.html}{\text{(3.12)}}\\ 20+6x-2x^2 &\geq 0 && \text{Via }f(x)=x-20\text{, increasing }\knowl{./knowl/eq_inc.html}{\text{(3.11)}}\\ x^2-3x-10 &\leq 0 && \text{Via }f(x)=-\frac12 x\text{, decreasing }\knowl{./knowl/eq_dec.html}{\text{(3.12)}}\\ \left(x-\frac32\right)^2 - \frac{49}{4} &\leq 0 && \text{Completing the square}\\ \left(x-\frac32\right)^2 &\leq \frac{49}{4} && \text{Via }f(x)=x+49/4\text{, increasing }\knowl{./knowl/eq_inc.html}{\text{(3.11)}}\\ \sqrt{\left(x-\frac32\right)^2} &\leq \frac{7}{2} && \text{Via }f(x)=\sqrt{x}\text{, increasing }\knowl{./knowl/eq_inc.html}{\text{(3.11)}}\\ \left|x-\frac32 \right| & \leq \frac72 && \knowl{./knowl/def_absolutevalue.html}{\text{Definition 3.7}}\\ -\frac72 \leq x-\frac32 &{} \leq \frac72 && \text{By }\knowl{./knowl/eq_abseq.html}{\text{(3.6)}}\\ -2 \leq{} x &{}\leq 5 && \text{Via }f(x)=x+\frac32\text{, increasing }\knowl{./knowl/eq_inc.html}{\text{(3.11)}} \end{align*}$

So interval notation for the solution set of this inequality would be $[-2,5]\text{.}$

🔗

Worksheet 3.4 Inequalities and Absolute Value Workbook

🔗

1.

Prove that for all $a,x\in\mathbb{R}\text{,}$ we have $|x|\leq a$ if and only if $-a \leq x \leq a\text{.}$

🔗

Use the above theorem to solve #2-4.

🔗

2.

If the distance between $x$ and $7$ is less than or equal to $3\text{,}$ what are the possible outcomes for $x\text{?}$

🔗

3.

Find all $x\in\mathbb{R}$ so that $\bigl|4x-11\bigr|\leq 10\text{.}$

🔗

4.

Find all $x\in \mathbb{R}$ so that $\bigl|9x+2\bigr| \leq 2\text{.}$

🔗

5.

Use the property

$\begin{equation*} \text{If } c\geq 0, \text{ then } |a|\leq c \text{ if and only if } -a \leq c \leq a \end{equation*}$

to solve the inequality $|a|\leq 5\text{.}$

🔗

6.

Use the triangle inequality to prove that for all $a,b,c\in\mathbb{R}\text{,}$

$\begin{equation*} \bigl|a+b+c\bigr| \leq |a|+|b|+|c|. \end{equation*}$

🔗

7.

Use the triangle inequality to prove: For all $a,b\in\mathbb{R}\text{,}$ we have

$\begin{equation*} |a|-|b| \leq |a+b| \leq |a|+|b|. \end{equation*}$

🔗

8.

Prove by induction that, for all $n\geq 2\text{,}$ if $a_1,a_2,a_3,\ldots,a_n\in\mathbb{R}\text{,}$ then

$\begin{equation*} \bigl|a_1+a_2+a_3+\cdots+a_n\bigr| \leq |a_1| + |a_2| + |a_3| + \cdots + |a_n|. \end{equation*}$

🔗

9.

Graph the piecewise function $f(x) = \begin{cases} x^2+1 & \text{when }x\lt 0\\ \frac12 x + 3 & \text{when }x \geq 0\end{cases}\text{.}$