Set Theory

Section 2 Set Theory

Subsection 2.1 Sets and Set Operations

A set \(A\) is a collection of elements for which the Law of Excluded Middle applies to their membership: Given any \(x\text{,}\) the answer to the question “Is \(x\) an element of \(A\text{?}\)” is either “yes” or “no”.

Remark 2.1. Important Sets to Know.

Real analysis is about the “set of real numbers”: where it comes from, and what properties it has. The following sets are useful to know along the way.

\begin{align} \mathbb{N} &= \{ 1, 2, 3, 4, \ldots \} && \text{The natural numbers}\tag{2.1}\\ \mathbb{Z} &= \{ \ldots, -2,-1,0,1,2,\ldots \} && \text{The integers}\tag{2.2}\\ \mathbb{Q} &= \left\{ \frac{p}{q} \colon p,q\in\mathbb{Z} \text{ and } q\neq 0 \right\} && \text{The rational numbers}\label{eq_rational}\tag{2.3}\\ \mathbb{I} = \mathbb{R}\setminus\mathbb{Q} &= \bigl\{ \ldots,\sqrt{2},\sqrt{3},e,\pi,\ldots,\bigr\} && \text{The irrational numbers}\tag{2.4} \end{align}

You may remember that rational numbers are exactly those that have “eventually repeating decimal expansions”. While this is true, it's almost always not the most helpful way to understand them and you should get used to using the above definition. You might want to forget, at least in the beginning, that numbers have decimal expansions at all!

Definition 2.2. Subset.

Let \(A,B\) be two sets. We say \(A\) is a subset of \(B\text{,}\) and write \(A\subseteq B\text{,}\) if every element of \(A\) is also an element of \(B\text{:}\)

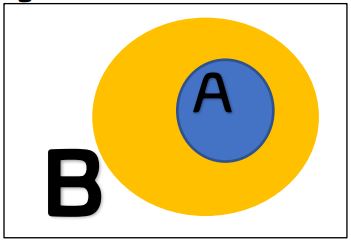
\begin{gather} (x\in A) \Rightarrow (x\in B).\label{eq_subset}\tag{2.5} \end{gather}

Definition 2.3. Equality of Sets.

Let \(A,B\) be two sets. We say that \(A\) is equal to \(B\text{,}\) and write \(A=B\text{,}\) if every element of \(A\) is also an element of \(B\text{,}\) and vice versa:

\begin{gather} A \subseteq B \text{ and } B\subseteq A.\label{eq_equality}\tag{2.6} \end{gather}

Definition 2.4. Universe.

A universe (or universal set) for a collection of sets \(A_1,A_2,A_3,\ldots\) is a set \(U\) of which all of the \(A_i\) are subsets:

\begin{equation*} A_i \subseteq U \qquad \text{for all }i=1,2,3,\ldots \end{equation*}

In the following definitions, let \(A,B\) be two sets and \(S\) be a universal set for \(A,B\text{,}\) that is, \(A,B \subseteq S\text{.}\)

Definition 2.5. Union.

The union of \(A\) and \(B\text{,}\) denoted \(A\cup B\text{,}\) is the set of all elements which either belong to \(A\text{,}\) belong to \(B\text{,}\) or belong to both sets:

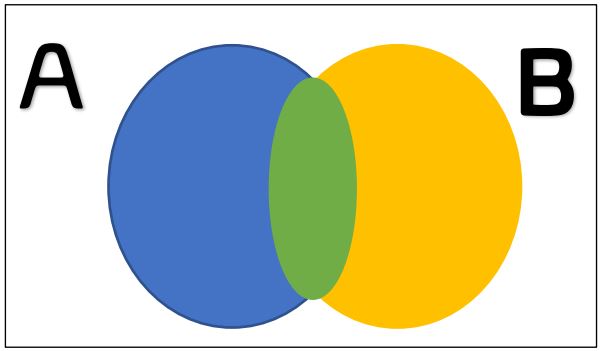
\begin{equation*} A\cup B = \bigl\{ x\in S \colon (x\in A) \vee (x\in B) \bigr\}. \end{equation*}

The union \(A\cup B\) consists of the blue, green, and yellow regions shaded above.

Definition 2.6. Intersection.

The intersection of \(A\) and \(B\text{,}\) denoted \(A\cap B\text{,}\) is the set of all elements which \(A\) and \(B\) have in common:

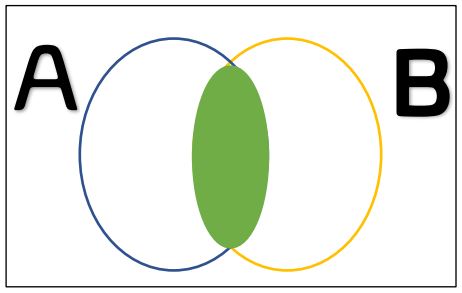
\begin{equation*} A\cap B = \bigl\{ x\in S \colon (x\in A) \wedge (x\in B) \bigr\}. \end{equation*}

The intersection \(A\cup B\) consists only of the green shaded region above.

Definition 2.7. Complement.

The complement of \(A\text{,}\) denoted \(A^C\text{,}\) is the set of all elements in the universe which do not belong to \(A\text{:}\)

\begin{equation*} A^C = \bigl\{ x\in S \colon x\not\in A \bigr\}. \end{equation*}

The complement \(A^C\) gives the universe surrounding \(A\text{.}\)

Definition 2.8. Difference.

The difference of \(A\) and \(B\text{,}\) denoted \(A\setminus B\text{,}\) is the set of all elements of \(A\) which are not elements of \(B\text{:}\)

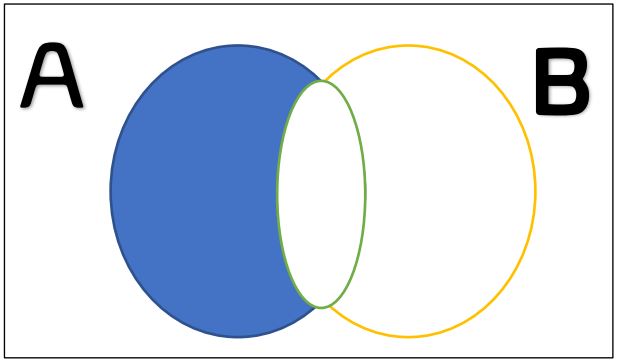
\begin{equation*} A\setminus B = \bigl\{ x\in S \colon (x\in A) \wedge (x\not\in B) \bigr\}. \end{equation*}

The set difference \(A\setminus B\) consists only of the blue region shaded above.

Remark 2.9.

Venn diagrams are helpful in understanding set algebra operations. In these examples, the indicated set consists of all the regions shaded in colors.

Figure 2.10. The set \((A\cup B)\setminus C\text{.}\)

Figure 2.11. The set \((A\cap C)\cup B\text{.}\)

The following theorem gives properties of these set operations.

Theorem 2.12. Set Algebra Properties.

Let \(A,B,C\) be sets. Then each of the following hold.

\begin{align} A\cup B &= B\cup A && \text{Commutative law for union}\label{eq_communion}\tag{2.7}\\ A\cap B &= B\cap A && \text{Commutative law for intersection}\label{eq_comminter}\tag{2.8}\\ A\cup (B\cup C) &= (A\cup B)\cup C && \text{Associative law for union}\label{eq_assocunion}\tag{2.9}\\ A\cap (B\cap C) &= (A\cap B)\cap C && \text{Associative law for intersection}\label{eq_associnter}\tag{2.10}\\ A\cup (B\cap C) &= (A\cup B)\cap(A\cup C) && \text{Distributive law for union}\label{eq_distunion}\tag{2.11}\\ A\cap (B\cup C) &= (A\cap B)\cup(A\cap C) && \text{Distributive law for intersection}\label{eq_distinter}\tag{2.12} \end{align}

Theorem 2.13. De Morgan's Laws for Sets.

Given two sets \(A,B\text{,}\) the following equalities hold:

The complement of a union is the intersection of complements:

\begin{equation*} \bigl(A\cup B\bigr)^C = A^C \cap B^C \end{equation*}
The complement of an intersection is the union of complements:

\begin{equation*} \bigl(A\cap B\bigr)^C = A^C \cup B^C \end{equation*}

Definition 2.14. Cardinality.

Let \(A\) be a set. The cardinality of \(A\text{,}\) denoted¹ by \(N(A)\text{,}\) is the number of elements in the set \(A\text{,}\) if this number is finite.

Other notations for cardinality include \(n(A), \#(A), \) and \(|A|\text{.}\)

Remark 2.15.

Let \(A= \bigl\{ x\in\mathbb{R} \colon x^2-2=0 \bigr\}\text{.}\) Then \(N(A)=2\text{,}\) because \(A\) has two elements:

\begin{equation*} A = \bigl\{ \sqrt{2}, -\sqrt{2} \bigr\}. \end{equation*}

Definition 2.16. Power Set.

Let \(A\) be a set. The power set of \(A\text{,}\) denoted \(\mathcal{P}(A)\text{,}\) is the set whose elements are exactly the subsets of \(A\text{.}\)

Remark 2.17.

Let \(A=\{a,b\}\text{.}\) Then we can list all the subsets of \(A\text{:}\)

\begin{equation*} \{a,b\}, \quad \{a\}, \quad \{b\},\quad \emptyset \end{equation*}

so the power set of \(A\) is

\begin{equation*} \mathcal{P}(A) = \bigl\{\, \{a,b\}, \{a\}, \{b\}, \emptyset\, \bigr\}. \end{equation*}

Warning 2.18.

Think twice before putting brackets around the empty set!

The set \(\emptyset\) has zero elements (is the empty set).

The set \(\{ \emptyset\}\) has one element (it's not empty: its element is “the empty set”)!

Subsection 2.2 Proofs Involving Sets

Definition 2.19. Proving set membership.

Let \(A\) be a set, and \(S\) be a universal set for \(A\text{.}\) Suppose there is a family of logical propositions \(P\colon S \to \{\text{true}, \text{false}\}\) which defines \(A\) via

\begin{equation*} A=\bigl\{ x\in S \colon P(x) \bigr\}. \end{equation*}

To prove that “\(a\) is an element of \(A\)” (or \(a\in A\)), we must establish two claims:

Show that \(a\) is an element of the universe (\(a\in S\)).
Show that \(P(a)\) is true.

Definition 2.20. Proving subset (“Element argument”).

Let \(A,B\) be sets. To prove the claim that “\(A\) is a subset of \(B\)” (or \(A\subseteq B\)), we must establish that every element of \(A\) is also an element of \(B\).

A direct proof of \(A\subseteq B\) is known as an element argument. It takes the form of a universal statement proof:

Let \(x\in A\) be chosen arbitrarily.
We wish to show that \(x\in B\) as well.
(Deduce that indeed, \(x\) is an element of \(B\text{.}\))
Since \(x\) was chosen arbitrarily, this shows that all elements of \(A\) are also elements of \(B\text{.}\) Hence \(A\) is a subset of \(B\text{.}\)

Definition 2.21. Proving set equality.

Let \(A,B\) be two sets. To prove the claim that “\(A\) is equal to \(B\)” (or \(A=B\)), we must establish both \(A\) is a subset of \(B\text{,}\) and vice versa.

In other words, to prove \(A=B\) we prove (separately!) that \(A\subseteq B\) and \(B\subseteq A\text{.}\) Often each step is done via an element argument, but remember we must show both ways separately. This establishes the biconditional statement

\begin{equation*} (x\in A) \Leftrightarrow (x\in B). \end{equation*}

Worksheet 2.3 Set Theory Workbook

In #1-3, sketch and shade a Venn diagram that represents the indicated set operation.

1.

For two sets \(A\) and \(B\text{,}\) the set \(A^C \cup B\text{.}\)

2.

For three sets \(A,B,C\text{,}\) the set \((A\cap B)\cup C\text{.}\)

3.

For three sets \(A,B,C\text{,}\) the set \((A\cap B)\cap C\text{.}\)

4.

Let \(A\) and \(B\) be sets. Prove that if \(A\cup B = \emptyset\text{,}\) then \(A=\emptyset\) and \(B=\emptyset\text{.}\)

Hint

Try a proof by contrapositive.

5.

Prove DeMorgan's Laws for Sets.

Hint

Use an element argument and establish both subset inclusions for each. You'll need to apply the logical version of De Morgan's Laws.

6.

Let \(A,B,C\) be three sets. Prove the distributive law for unions over intersections:

\begin{equation*} A\cup(B\cap C) = (A\cup B) \cap (A\cup C). \end{equation*}

Hint

Use an element argument and establish both subset inclusions. This means proving both:

\begin{align*} \forall x\in A\cup(B\cap C), & \text{ we have } x\in (A\cup B)\cap (A\cup C) &\text{ and }\\ \forall x\in (A\cup B)\cap (A\cup C), & \text{ we have } x\in A\cup (B\cap C). \end{align*}

7.

What is the cardinality of each of the following sets?

\(\displaystyle A=\{0,2,4,6,8,\ldots,24\}\)
\(\displaystyle B = \bigl\{ \emptyset \bigr\}\)
\(\displaystyle C=\bigl\{ \, \{1,2,3\}, \{4,5,6\} \, \bigr\}\)
\(P(K)\text{,}\) with \(K = \{a,b,c\}\text{.}\)

8.

Let \(S\) be the universe where \(A,B,C\subseteq S\text{.}\) Let

\begin{align*} S &= \{1,2,3,4,5,6,7\}\\ A &= \{1,2,4\}\\ B &= \{1,3,5,7\}\\ C &= \{2,4,6,7\} \end{align*}

Find each of the following. Drawing a Venn diagram will help!

\(\displaystyle A\cup B\)
\(\displaystyle (A\cup B)\cap C\)
\(\displaystyle C^C \cup B\)
\(\displaystyle (A\cap B)^C\)
\(\displaystyle C\setminus B\)