Skip to main content

Section 13.3 Venn Diagrams

To visualize the interaction of sets, John Venn in 1880 thought to use overlapping circles, building on a similar idea used by Leonhard Euler in the 18th century. These illustrations are now called Venn diagrams.

Definition 13.3.1.

A Venn diagram represents each set by a circle, usually drawn inside of a containing box representing the universal set. Overlapping areas indicate elements common to both sets.

Basic Venn diagrams can illustrate the interaction of two or three sets.

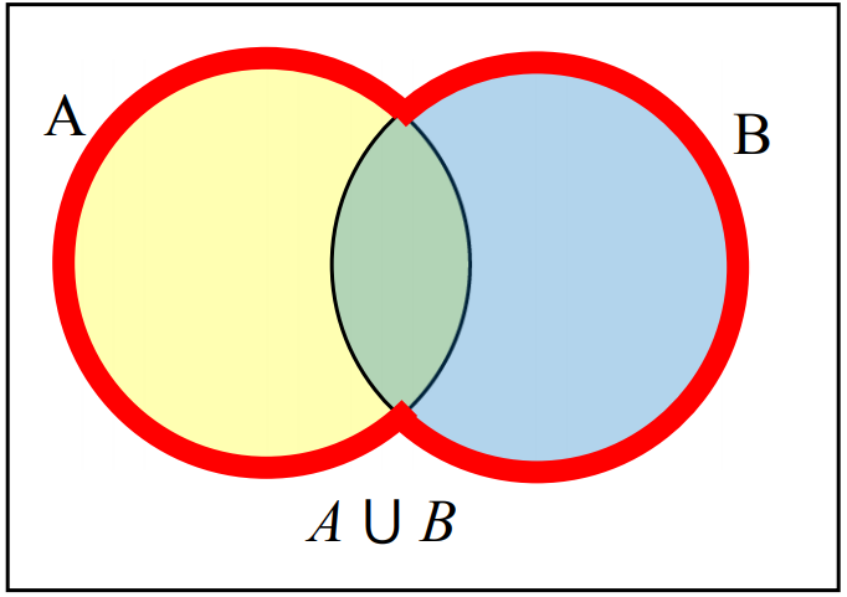
Example 13.3.2.

Create Venn diagrams to illustrate \(A\cup B\text{,}\) \(A\cap B\text{,}\) and \(A^c \cap B\text{.}\)

Figure 13.3.3. \(A\cup B\) contains all elements in either set.
Figure 13.3.4. \(A\cap B\) contains only those elements in both sets – in the overlap of the circles.
Figure 13.3.5. \(A^c\) will contain all elements not in the set \(A\text{.}\) \(A^c\cap B\) will contain the elements in set \(B\) that are not in set \(A\text{.}\)
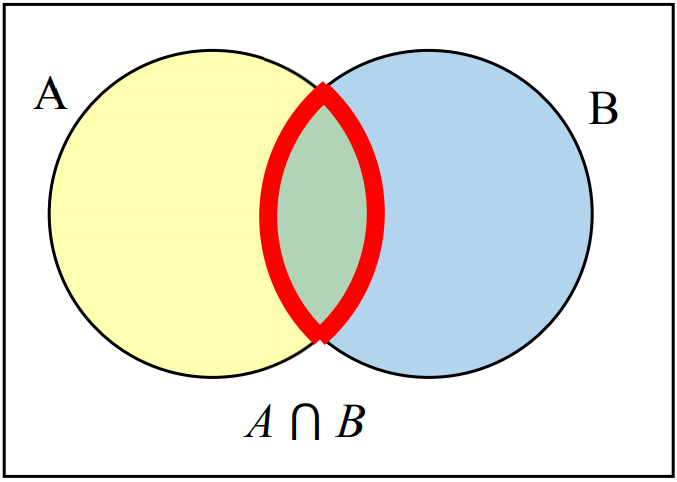
Example 13.3.6.

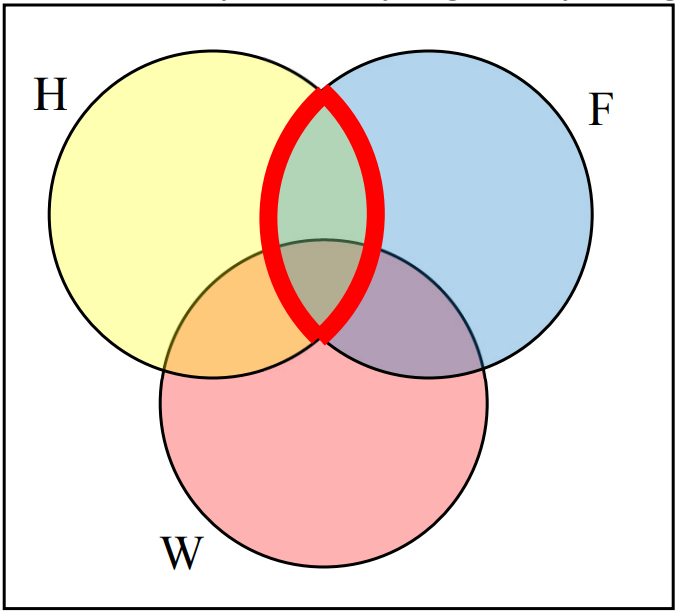
Use a Venn diagram to illustrate \((H\cap F)^c \cap W\text{.}\)

We’ll start by identifying everything in the set \(H\cap F\text{.}\)

Now, \((H\cap F)^c \cap W\) will contain everything not in the set identified above that is also in set \(W\text{.}\)

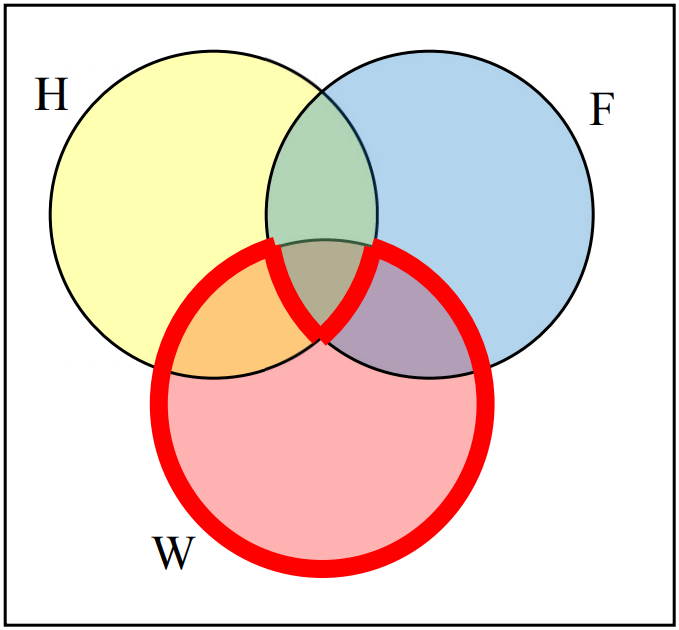
Example 13.3.7.

Create an expression to represent the outlined part of the Venn diagram shown.

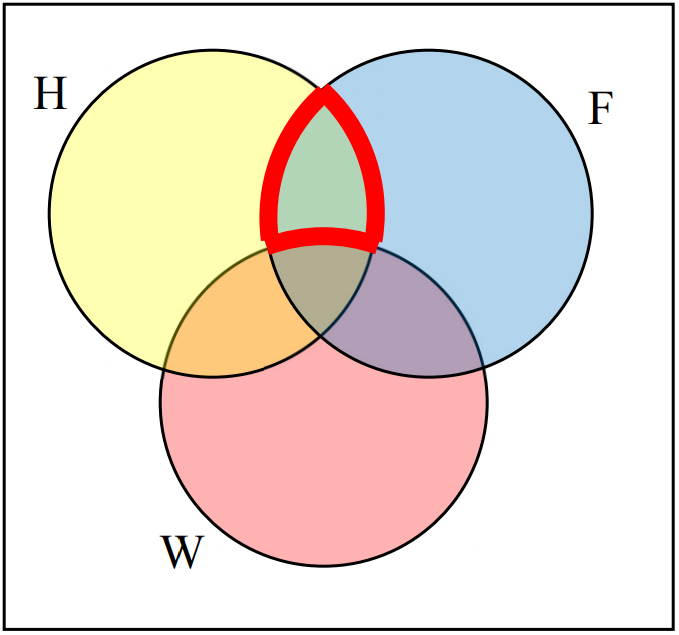
The elements in the outlined set are in sets \(H\) and \(F\text{,}\) but are not in set \(W\text{.}\) So we could represent this set as

\begin{equation*} H\cap F \cap W^c . \end{equation*}

Create an expression to represent the outlined portion of the Venn diagram shown.

Answer

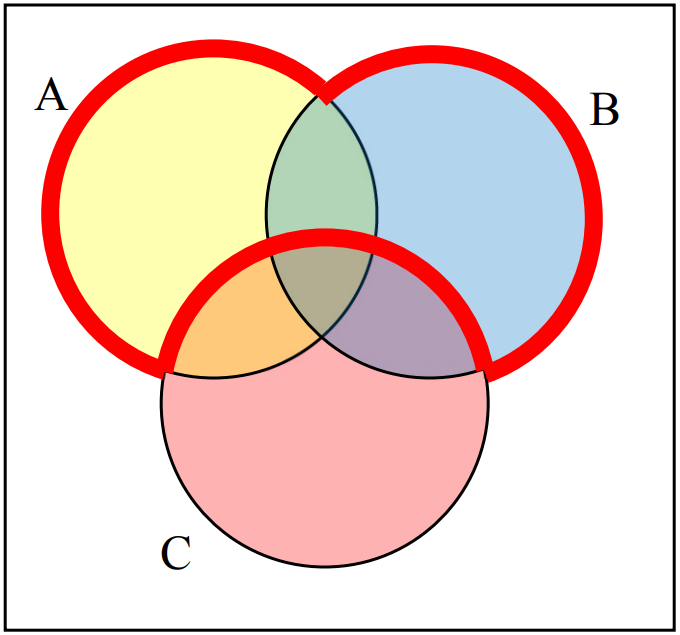
\(A\cup B \cap C^c\)

Exercises 13.3.1 Exercises

Create a Venn diagram to illustrate each of the following.

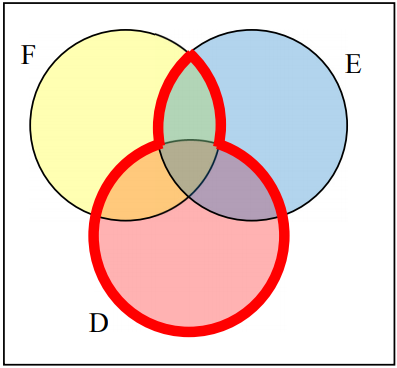
1.

\((F\cap E)\cup D\)

Answer

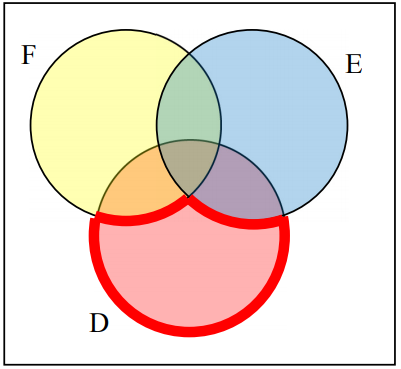
2.

\((D\cup E)^c\cap F\)

3.

\((F^c\cap E^c)\cap D\)

Answer

4.

\((D\cup E)\cup F\)

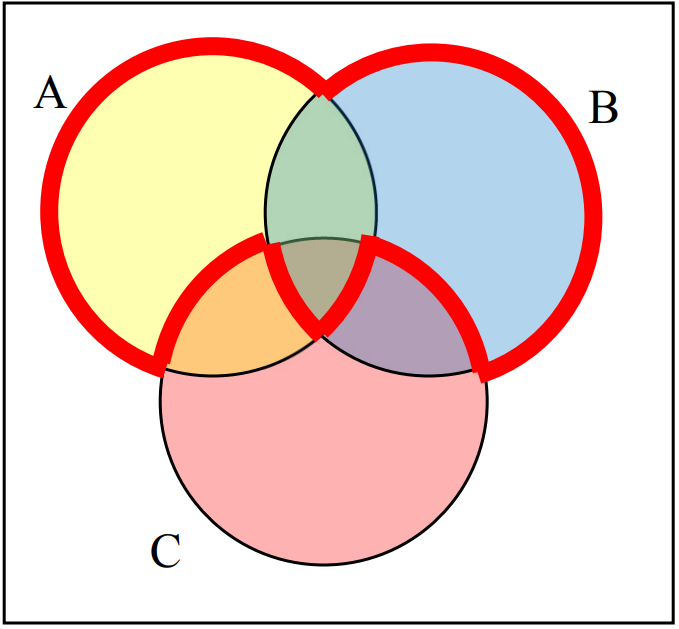
Write an expression for the shaded region.

5.
Answer

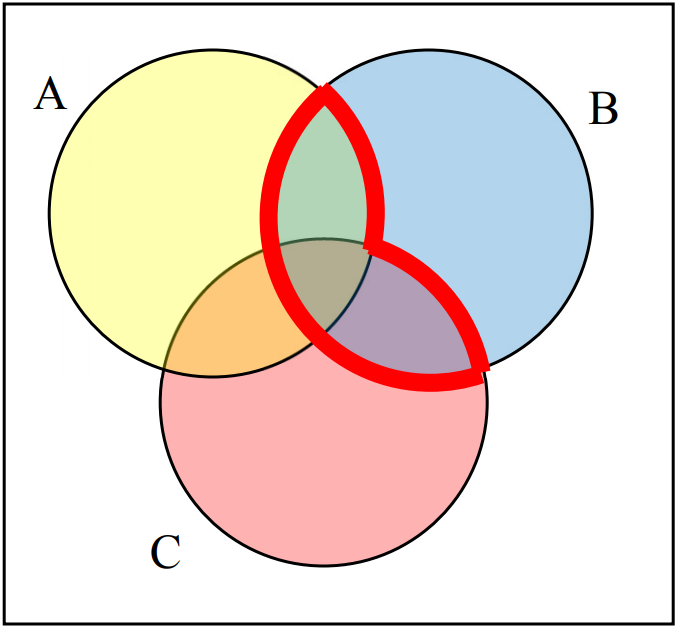
One possible answer: \((A\cap B)\cup(B\cap C).\)

6.
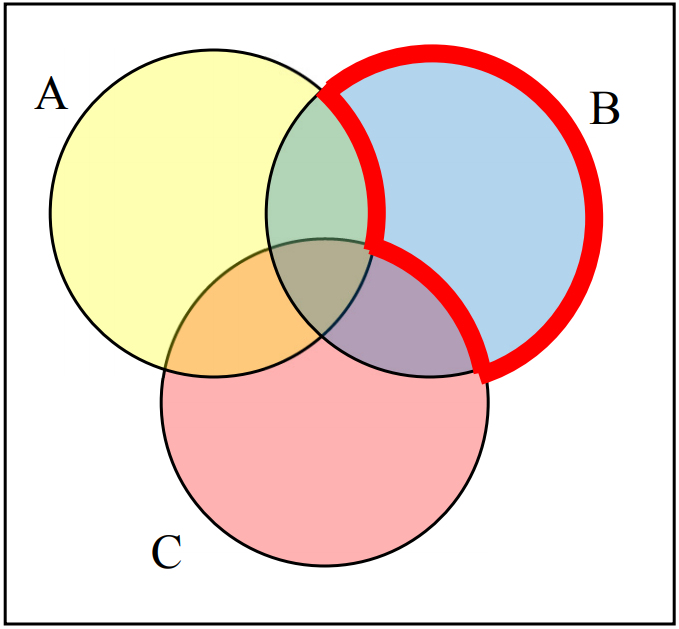
7.
Answer

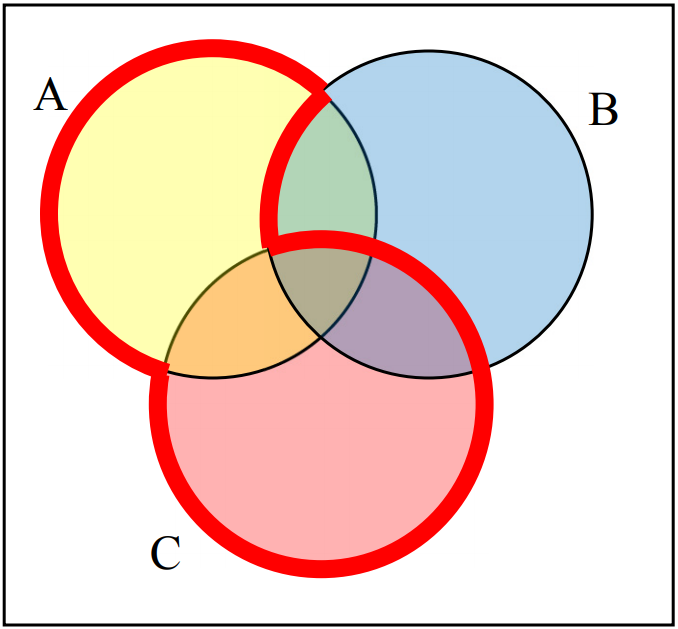
\((A\cap B^c)\cup C\text{.}\)

8.